PowerPC Tutorial

Previous Chapter

Chapter 21: Float Stores, Loads, & Conversions

Section 1: Fundamentals

Now lets get into floating point loads & stores. Here's are the key fundamentals...

Similar to GPR Loads & Stores, an EA must be calculated
Similar to GPR Loads & Stores, the source register(s) are GPRs
Similar to GPR Loads & Stores, the EA is rA + SIMM, or rA + rB

While we can obviously see how FPR loads & stores are similar to the GPR type, there is one super important difference.

The EA of *any* FP load/store *MUST* be divisible by 4 or else an Alignment exception will occur.

Section 2: Loads

With the fundamentals out of the way, let's get into real FP Loads/Stores.

Load Floating Point Single:

lfs fD, SIMM (rA) #EA = rA + SIMM

What occurs--

The EA is calculated by rA + SIMM
The 32-bit Single Float value located at the EA is loaded into fD.
It is converted to its 64-bit equivalent when it is placed in fD.

Lets go over an example...

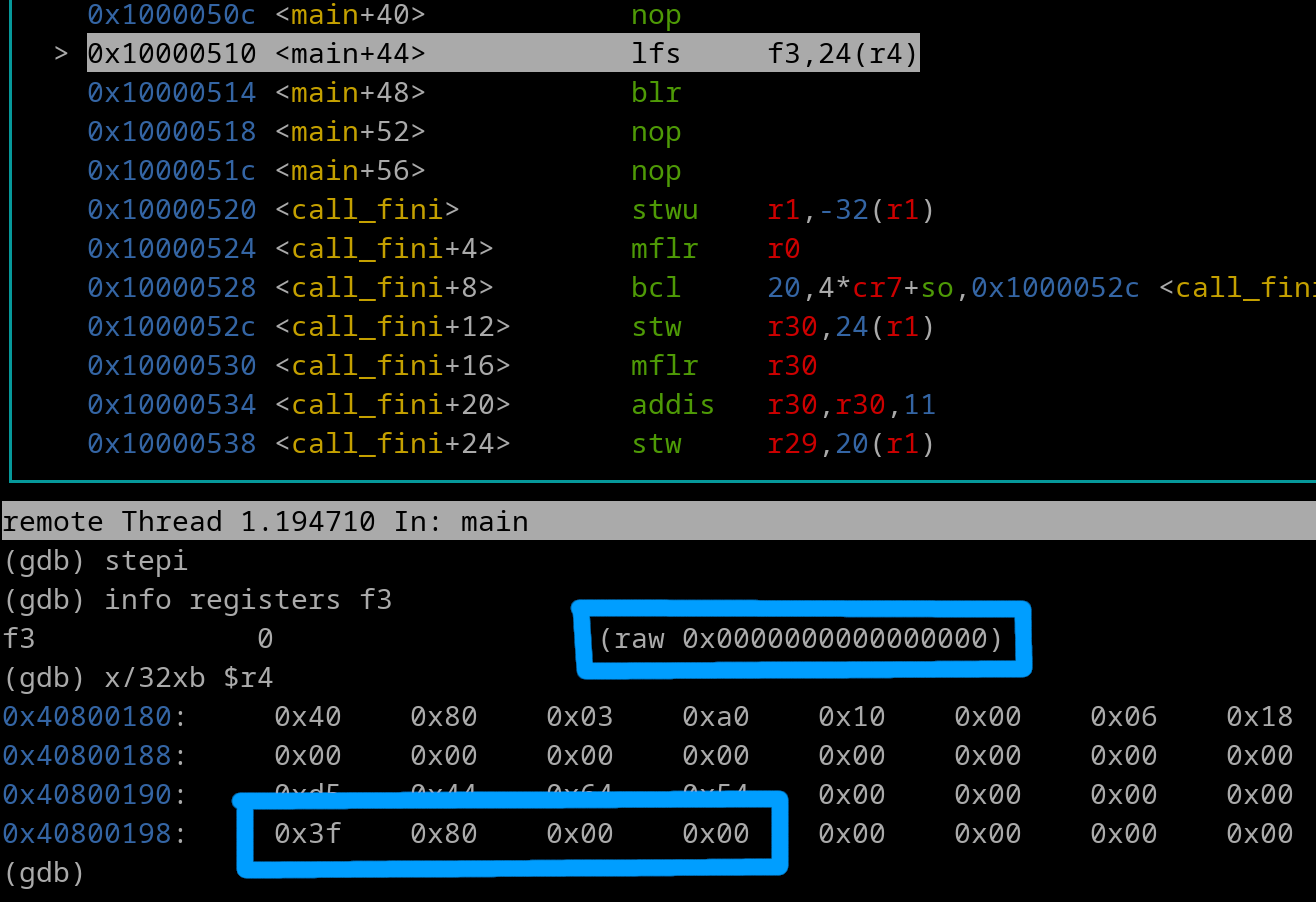
lfs f3, 0x0018 (r4)

Pretend r4 = 0x40800180
Pretend 32-bit float located at EA is 0x3F800000 (1.0)

Calculate the EA as usual (0x40800180 + 0x18). EA = 0x40800198

Here's a pic of right before the lfs instruction gets executed..

Now lets execute the lfs instruction...

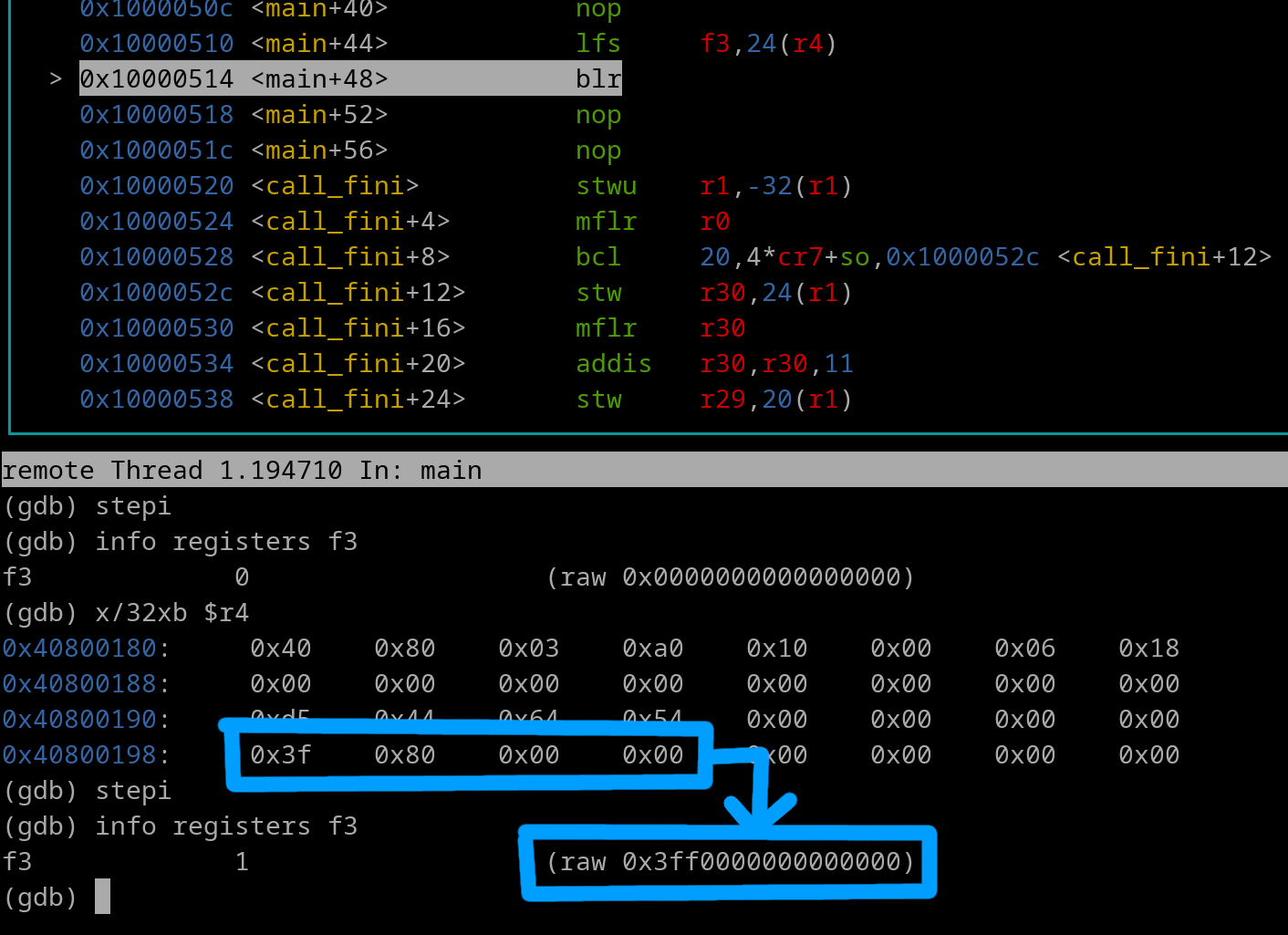
Notice how what gets loaded in the FPR is 0x3FF0000000000000. This is the 64-bit equivalent of 0x3F800000. Both are the decimal value of 1.0.

Load Floating Point Double:

lfd fD, SIMM16 (rA) #EA = rA + SIMM16

The 64-bit float value located at the EA is loaded in fD. Let's go over a quick example.

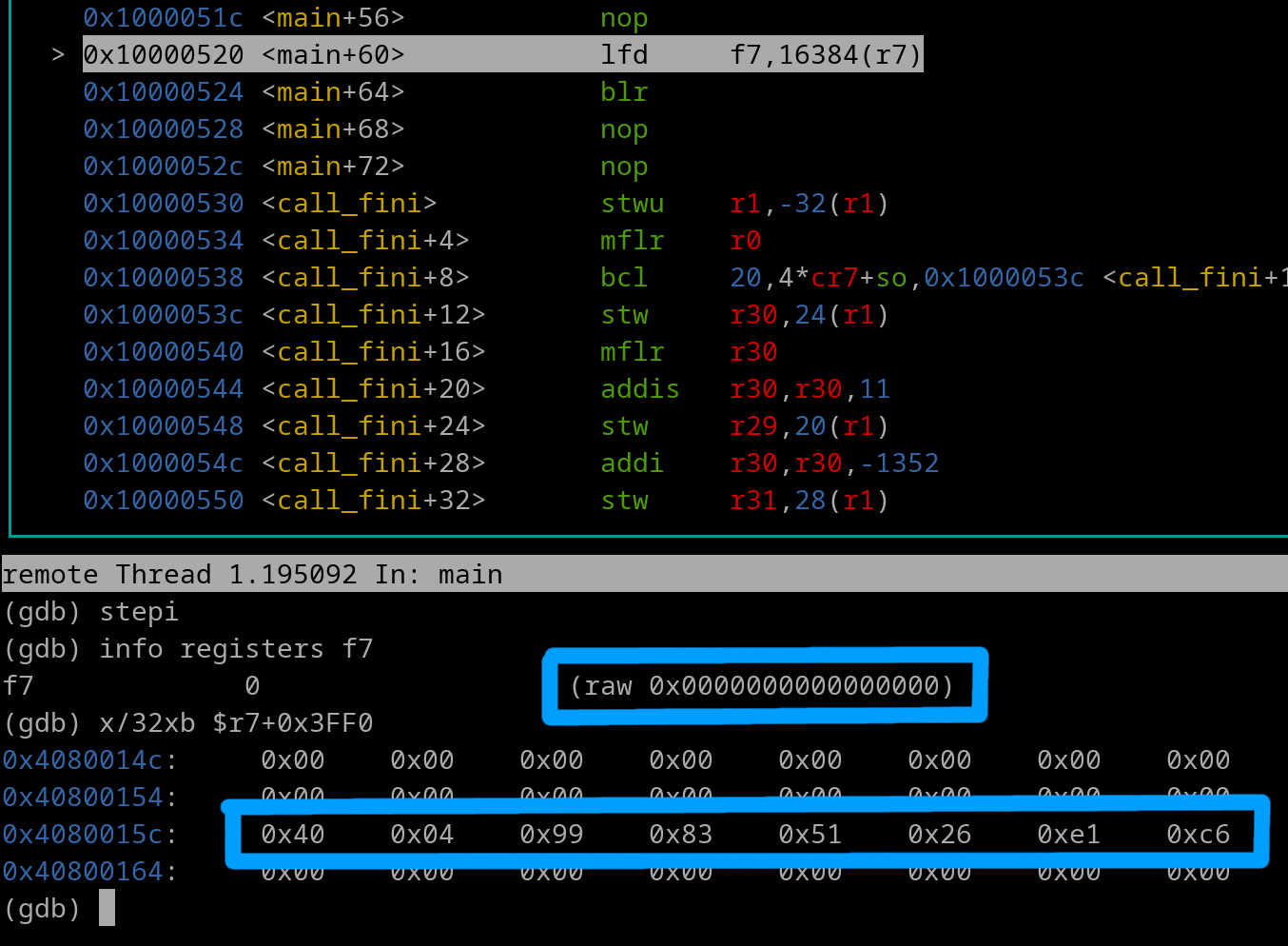
Pretend that r7 = 407FC15C
Pretend that the 64-bit float at the EA is 0x400499835126E1C6
Our instruction is the following....

lfd f7, 0x4000 (r7)

We calculate the EA which is r7 + 0x4000. The EA is 0x4080015C. The 64-bit value located at that EA is placed into f7. Here's a pic of right before the lfd instruction gets executed.

Now lets execute the lfd instruction...

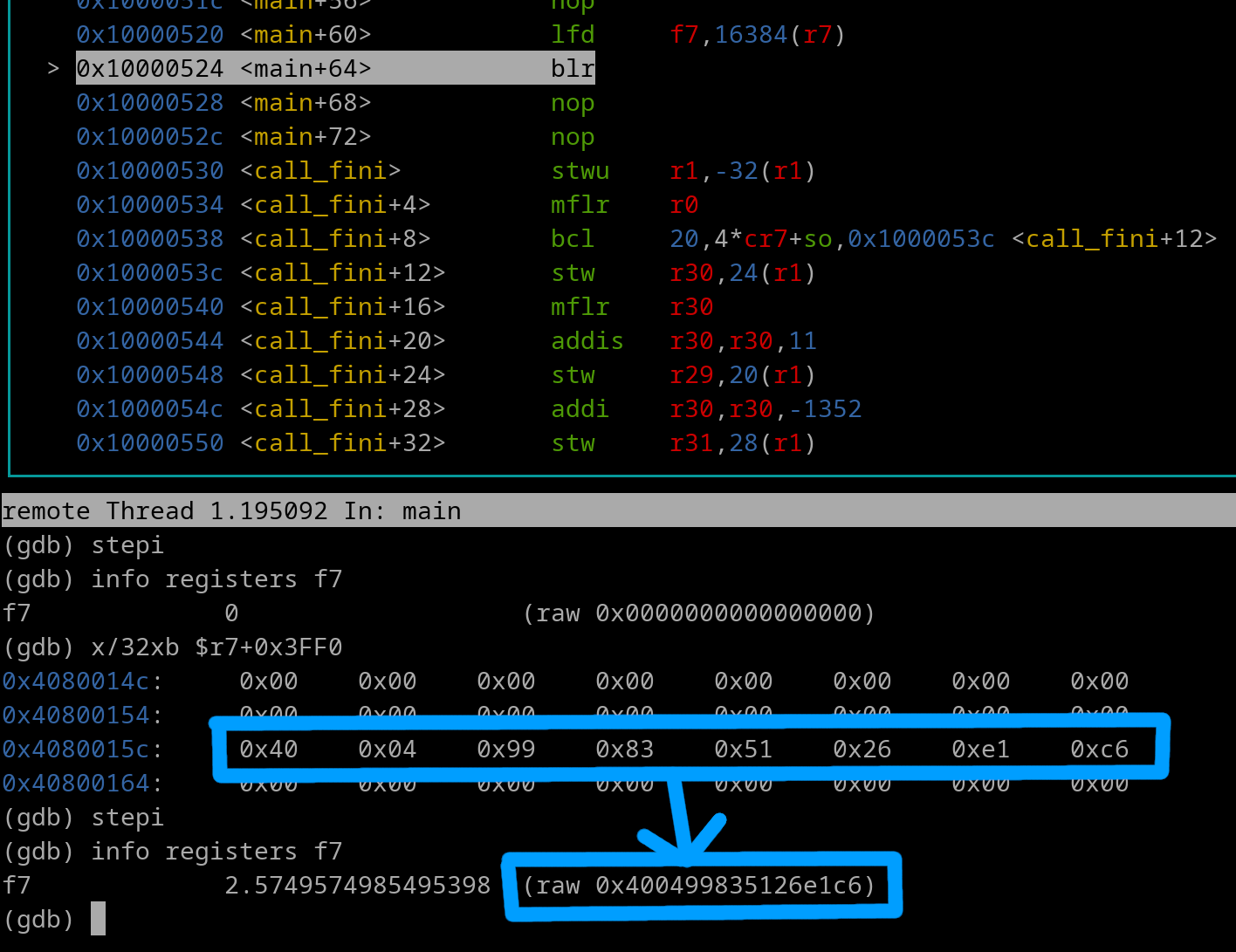
We see the 64-bit float was loaded from Memory into f7.

Just like with GPR loads & stores, you have indexed and update type loads.

Load Floating Pointer Single Indexed:
lfsx fD, rA, rB #EA = rA + rB

Load Floating Point Double Indexed:
lfdx fD, rA, rB #EA = rA + rB

Load Floating Point Single Update:
lfsu fD, SIMM (rA) #EA = rA + SIMM

Load Floating Point double update:
lfdu fD, SIMM (rA) #EA = rA + SIMM

Section 3: Stores

Store Floating Point Single:

stfs fD, SIMM (rA) #EA = rA + SIMM

What occurs~

The 64-bit float is converted to its 32-bit equivalent
***If the 64-bit float was of double precision, it is rounded to single precision when converted
The 32-bit single float is stored at the EA

***NOTE: Certain PowerPC chips may have their own quirks. For example, on Broadway (PPC Chip of the Nintendo Wii) if a Denormalized Double Float is stored via stfs, the value of 0x00000000 is stored. We haven't discussed Denormalized floats in detail as that's not the point of this note. What's key here is you need to know is that it's considered a programming/coding error to use stfs to store double-precision floats.

Let's go over an example:

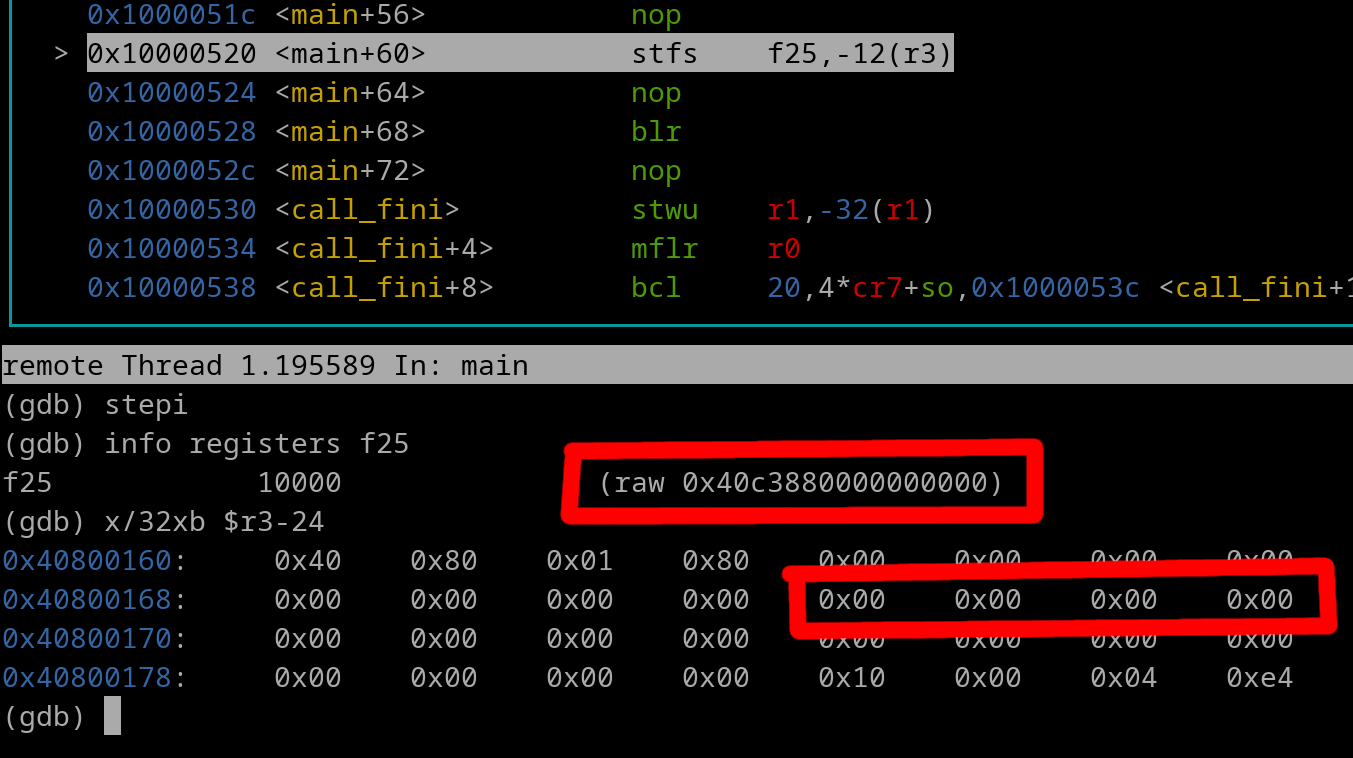
stfs f25, -0xC (r3)

Pretend that...
r3 = 0x40800178
f25 = 0x40C38800000000000 (10000.0)

As usual the EA gets calculated. 0x40800178 - 0xC = 0x4080016C
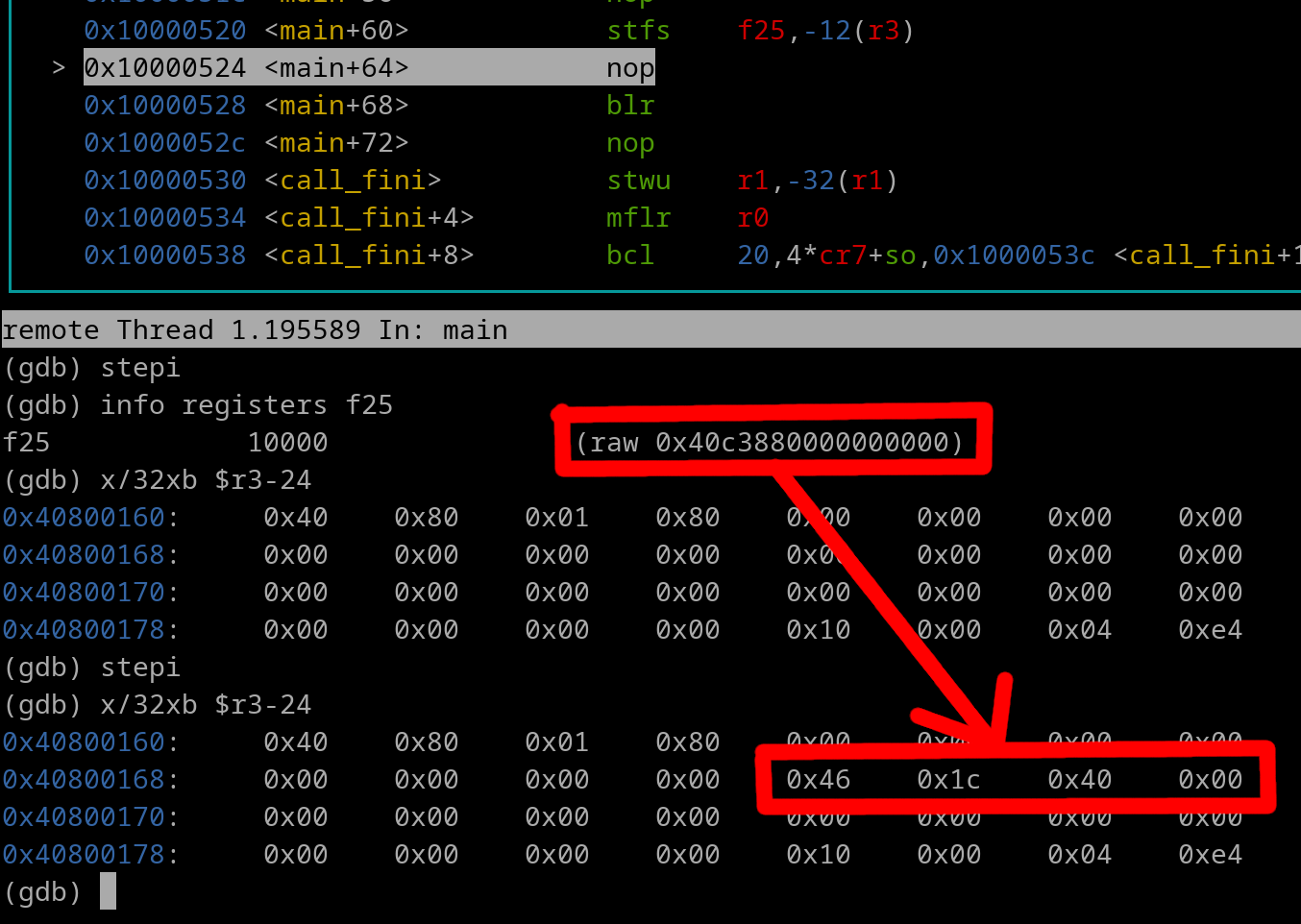
The 64-bit single float gets converted to its 32-bit form which is 0x461C4000
THe 32-bit float 0x461C4000 gets stored at address 0x4080016C

Here's a pic of right before the stfs instruction gets executed...

Now let's execute the stfs instruction...

Store Floating Point Double:

stfd fD, SIMM (rA) #EA = rA + SIMM

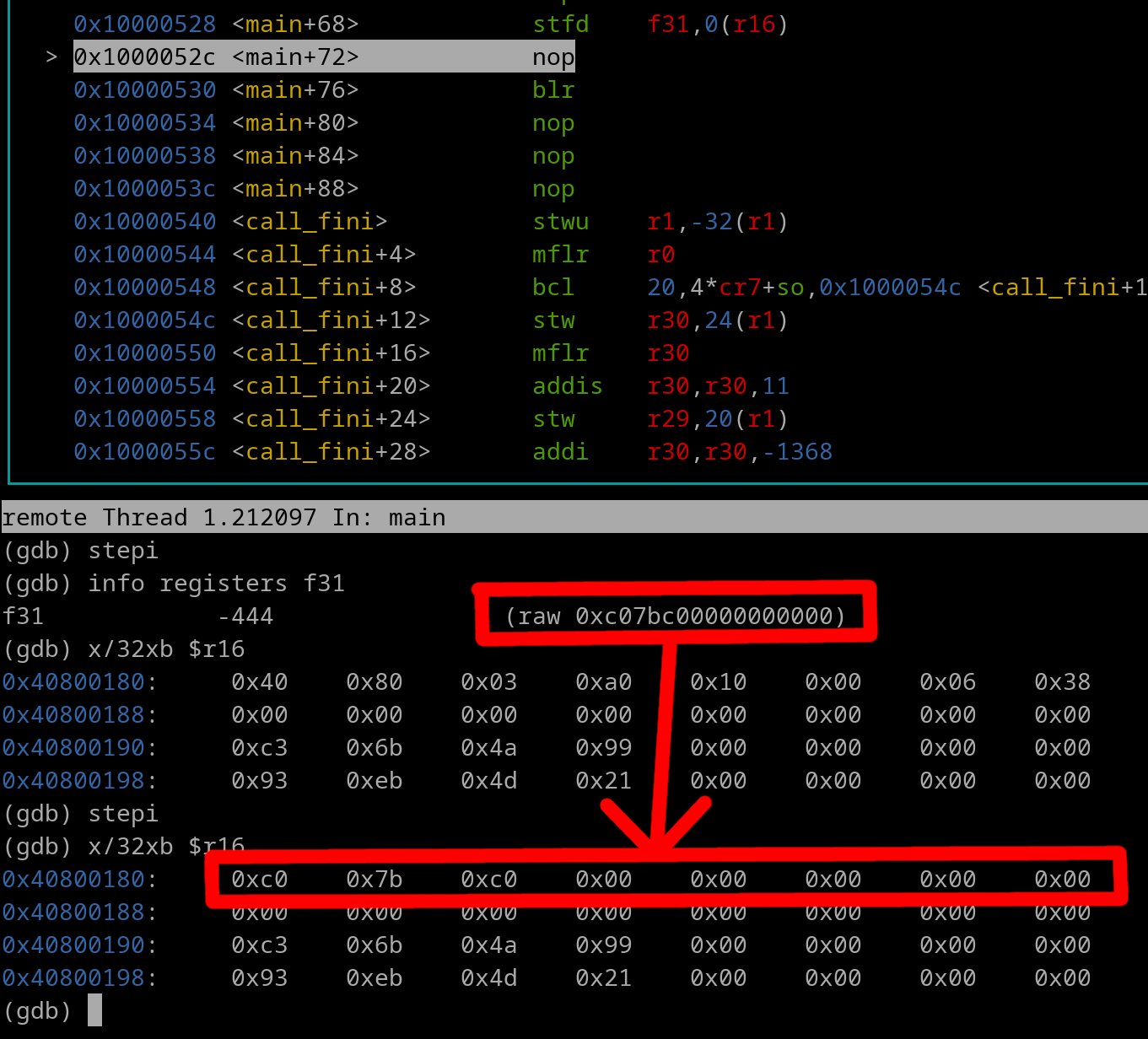
The 64-bit float gets stored at the EA

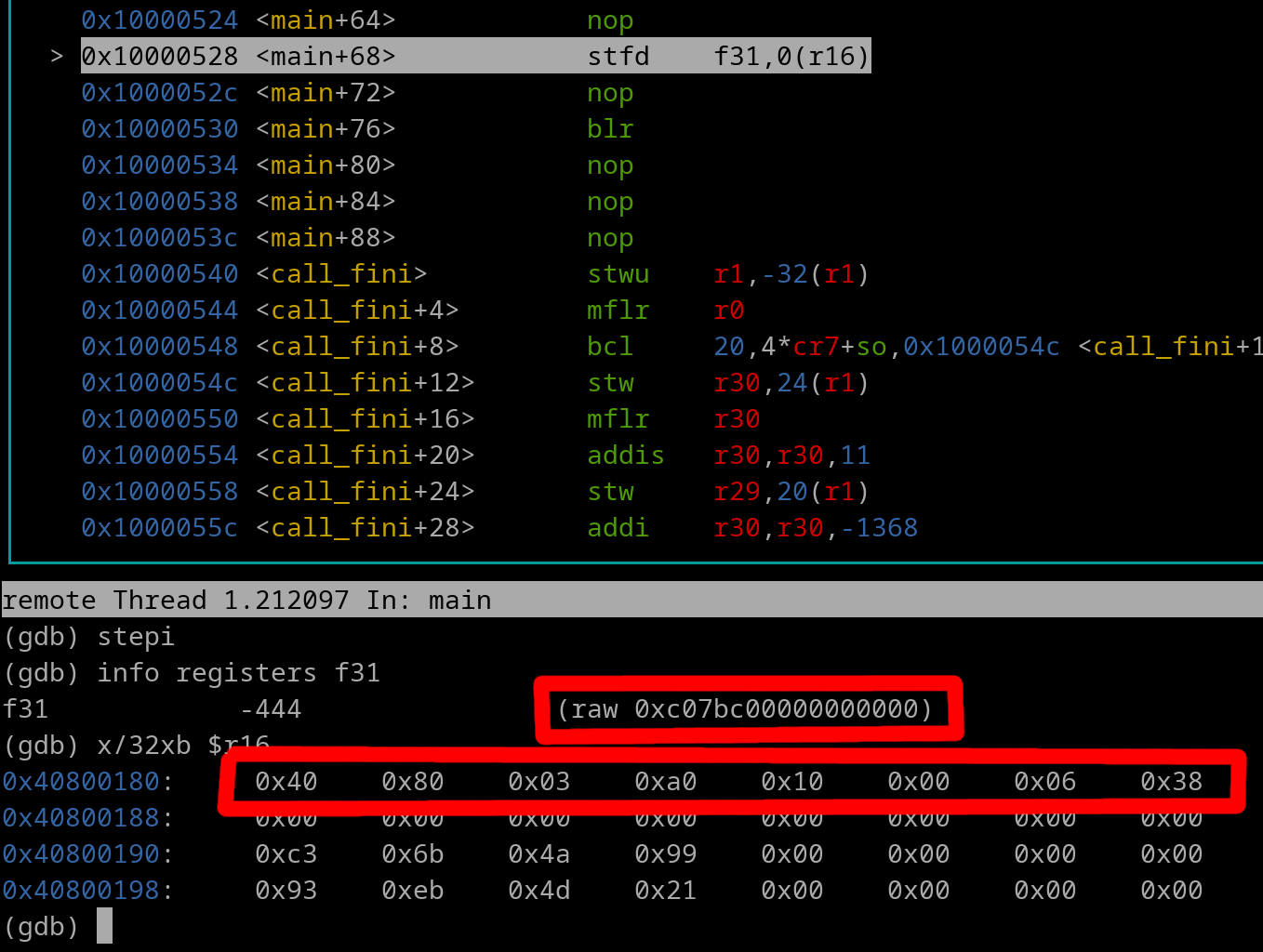
Quick example:
Pretend r16 = 0x40800180
f31 = 0xC07BC00000000000

stfd f31, 0 (r16)

Pic right before instruction lfd executes:

Pic once stfd instruction has executed:

Here are some other FP store instructions~

Store Floating Pointer Single Indexed:
stfsx fD, rA, rB #EA = rA + rB

Store Floating Point Double Indexed:
stfdx fD, rA, rB #EA = rA + rB

Store Floating Point Single Update:
stfsu fD, SIMM (rA) #EA = rA + SIMM

Store Floating Point double update:
stfdu fD, SIMM (rA) #EA = rA + SIMM

Section 4: Loops

For most loops, the GPRs are used for transferring data. However for some PowerPC systems, you can use FP loads & stores to transfer integer data. This would result in a faster executing loop.

For example. Let's say we want to transfer 20 words of data using a loop. It would look typically like this...

.set src_address, 0x80001500
.set dst_address, 0x80456780
li r5, 20
mtctr r5
lis r4, src_address-4@h
ori r4, r4, src_address-4@l
lis r3, dst_address-4@l
ori r3, r3, dst_address-4@l
typical_loop:
lwzu r0, 0x4 (r4)
stwu r0, 0x4 (r5)
bdnz+ typical_loop

You can instead write it out like this using double-float loads and stores...

.set src_address, 0x80001500
.set dst_address, 0x80456780
li r5, 10 #20 words = 10 double-words
mtctr r5
lis r4, src_address-8@h #Minus 8 because double float is 8 bytes in width
ori r4, r4, src_address-8@l
lis r3, dst_address-8@l
ori r3, r3, dst_address-8@l
faster_loop:
lfdu r0, 0x8 (r4) #SIMM of 8 because double float is 8 bytes in width
stfdu r0, 0x8 (r5)
bdnz+ faster_loop

HOWEVER!!! In some PowerPC systems, this won't work. Why not? For example in the PPC Chip of the Nintendo Wii, if a Denormalized Float is stored via *any* double-float store instruction (i.e. stfdu), the Float gets converted to a Normalized Float when it gets stored to Memory.

In "nooby" terms, the data gets altered. What gets pasted won't be exactly what was initially copied. For those type of PPC systems, you can only use integer-type loops.

Question: Vega, how do I transfer floating point values if I can only use integer-type loops?

Answer: You still use the typical integer-type loops. The data remains intact regardless of whether its an integer or floating point value(s).

Question: Vega, let's say my PowerPC system can safely use those double-float loops. What about single-float loops transferring single-float values across Memory? Can I do that?

Answer: NO! Either use double-float loop to copy-paste two singles for each loop iteration, or stick with the typical integer-type loop.

Section 5: Conversions

Yes, you can convert float numbers to integers...

Floating Point Convert to Integer Word:

fctiw fD, fA

This will convert fA into an integer value and store the result into the lower 32-bits of fD. The upper 32 bits are left undefined (junk). Standard rounding is applied here.

Floating Point Convert to Integer Word Towards Zero:

fctiwz fD, fA #Notice the "z" in the mnemonic

Same as above fctiw except rounding is towards zero. Meaning 5.7 rounds to 5, and -4.2 rounds to -4.

Once that you have converted the float to an int, we need to way to store it memory.

Store Float Integer Word Indexed:

stfiwx fD, rA, rB #EA = rA + rB

NOTE: This instruction will ONLY store the LOWER 32-bits of fD to the EA.

Here's an example of having the float value of 2.75. Converting it to an int using standard rounding, Storing it to memory, then loading the integer into a GPR.

Pretend the 2.75 value resides in f5. Pretend memory at address 0x80451110 the EA. We will use r10 to load the int into.

fctiw f5, f5 #Convert 2.75 from float to int; use standard rounding
lis r3, 0x8045 #Set upper bits of EA
li r4, 0x1110 #Set lower bits of EA
stfiwx f5, r3, r4 #Store int to EA
lwzx r10, r3, r4 #Load int into GPR

Let's go over some images for a better look. Here's a pic of right before the fctiw gets executed. We see our 64-bit float (0x4006000000000000) in f5.

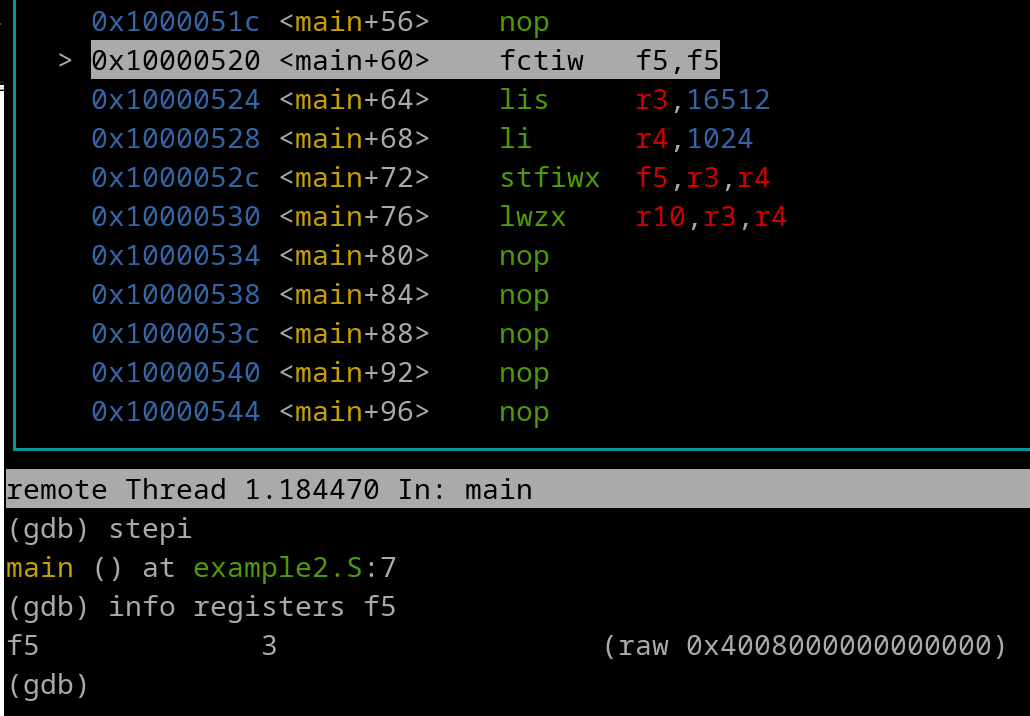
Let's execute the fctiw instruction and take a look...

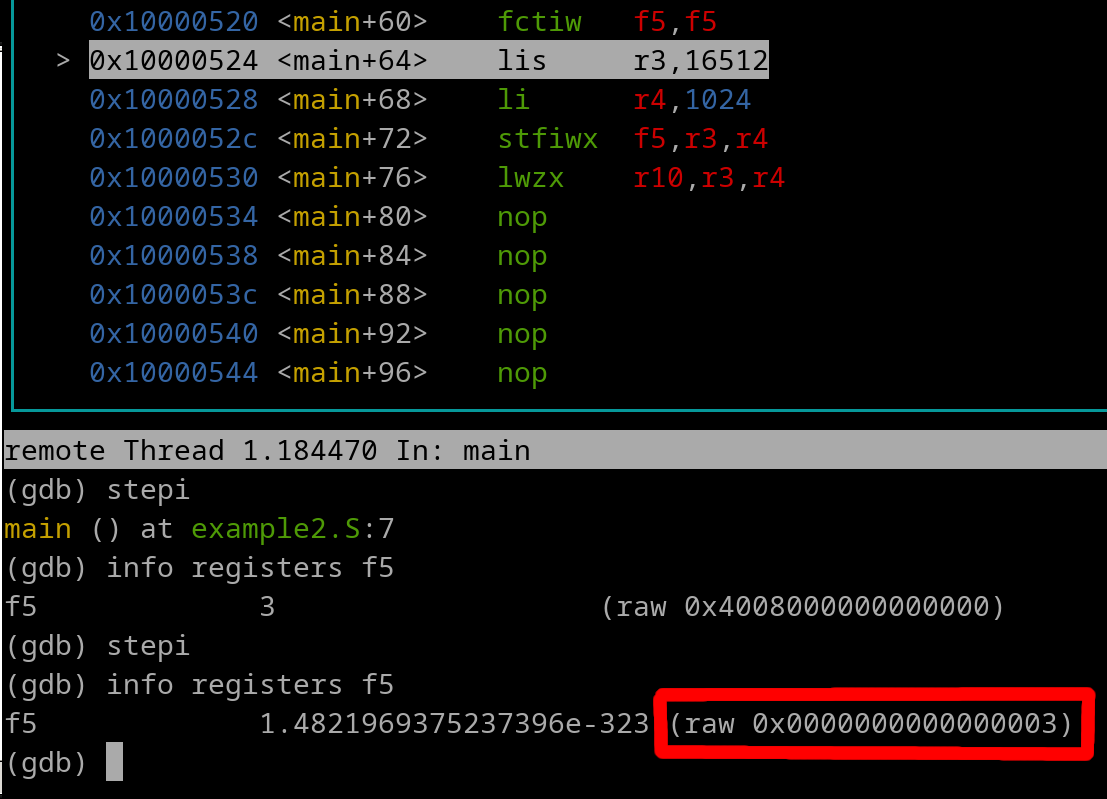
We see the lower 32-bits of f5 is (outlined in red) now 0x00000003 with the upper 32-bits being undefined (junk, 0x00000000 for this particular case). Lets go forward to right before the stfiwx gets executed...

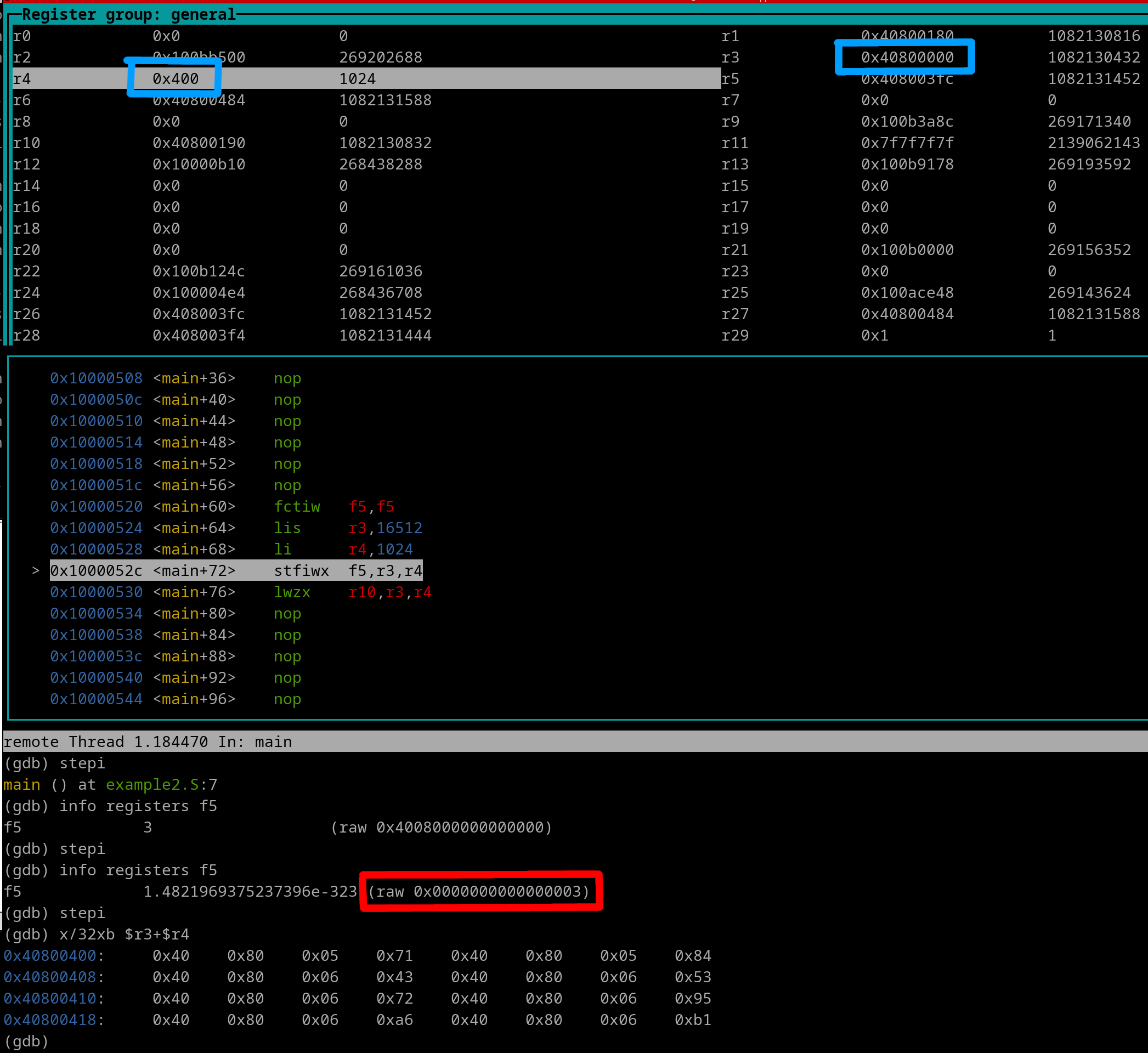
We see f5 contains our integer and that r3 + r4 is the Effective Address. f5 is outlined in red. r3 and r4 are outlined in blue. Let's execute the stfiwx instruction now...

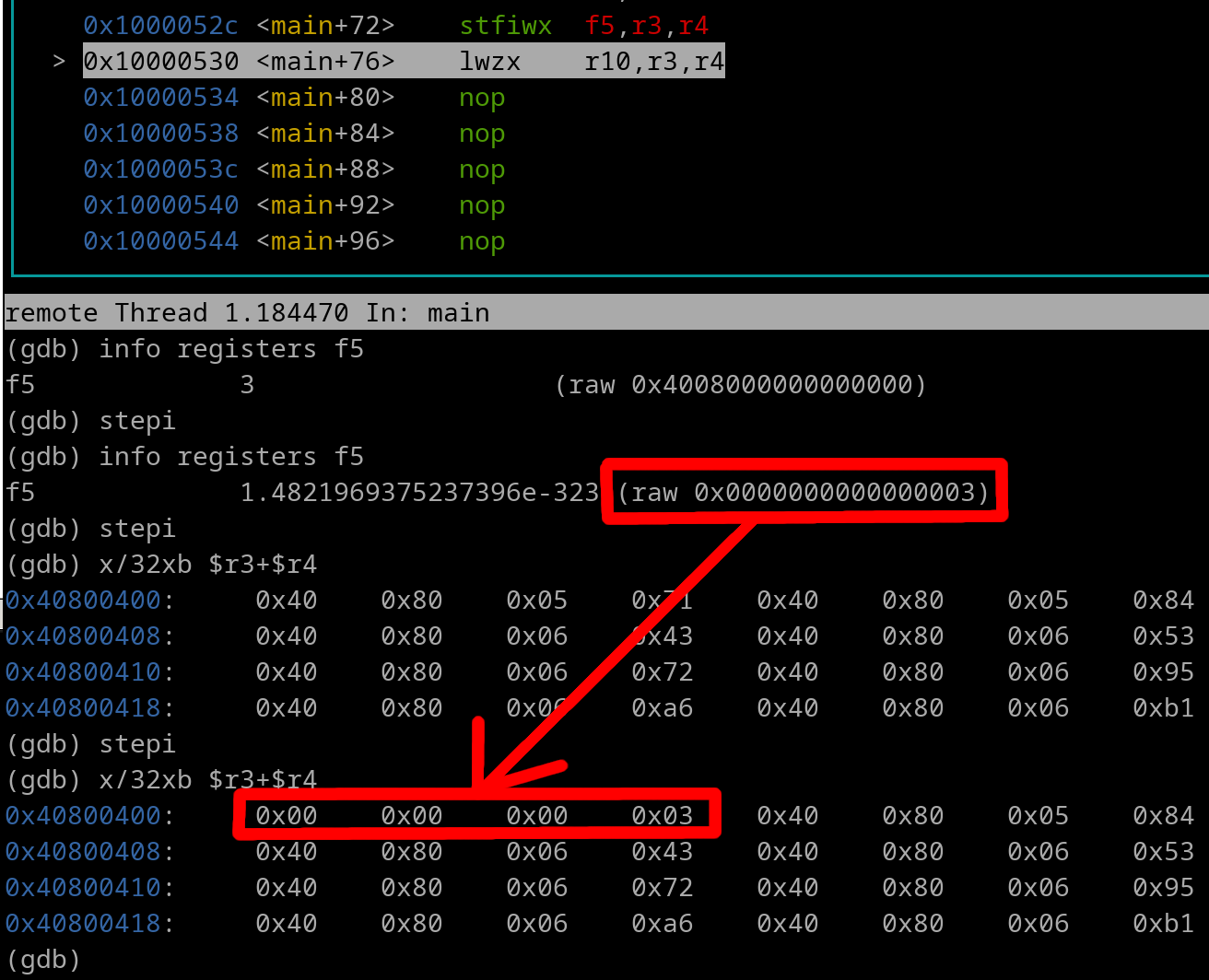
We see that 0x00000003 was stored at the EA. Let's now load it into r10....

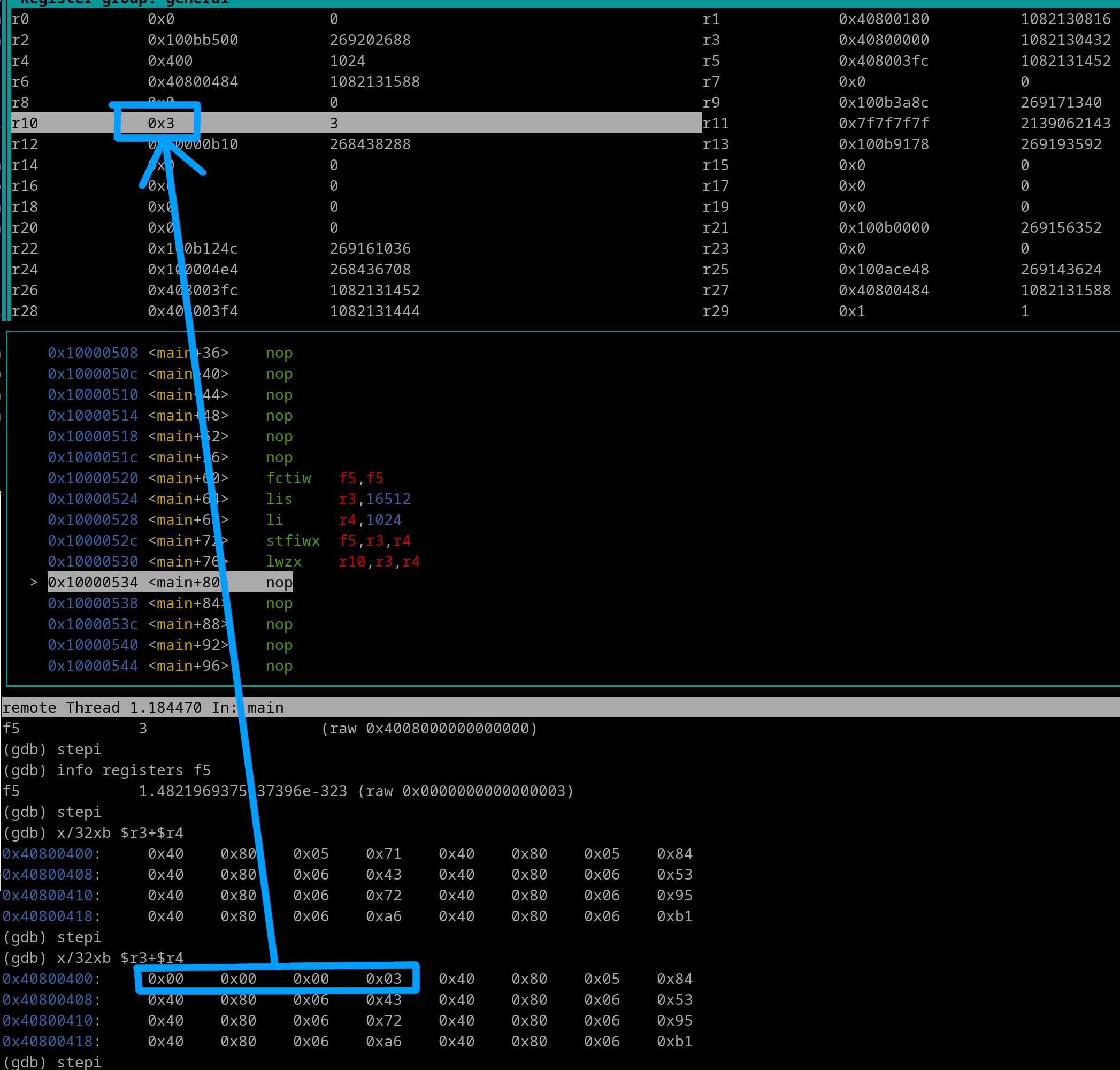
And there we go. The float was converted to an integer, and is now sitting in a GPR. R

Next Chapter

Tutorial Index