Chapter 20: Float Basics
I would assume a majority of you are here because you want to learn PowerPC for the Nintendo Wii or Gamecube. Well, what sucks for you all is that the behavior of Floating Pointer Instructions will vary depending on a Wii/Gamecube unique Special Purpose Register called "HID2". To keep it short, the PowerPC Chips for the Gamecube & Wii introduced an instruction set known as Paired Singles. Basically paired-single instructions are float instructions that can operate on two float values at the same time. Because of this instruction set, the HID2 SPR was placed in that allows the developers to turn it on/off.
With all that being said, I will be teaching you about Floats as if this HID2 register doesn't exist. Keep in mind, this will NOT accurately represent the standard behavior of the Gamecube/Wii.
Yes this sucks, but writing out 2 separate tutorials for every Float Chapter would not be ideal.
There are 32 Floating Pointer Registers (FPRs). f0 thru f31. The values in these registers can show partial numbers (i.e. 5.712, 4.5, 0.01, etc). Each FPR is 64-bits in width.
Here's a good online floating point decimal to hex converter - LINK
To see the floating pointer registers, type the following command in GDB...
info float
GDB will show each FPR in two different formats. The FPR's value in signed decimal first then the FPR's actual/raw 64-bit Hex Value.
Signed vs Unsigned Values:
Floating Point values are ALWAYS signed. A quick way to know if a Float Value is negative is to take a look at bit 0. If it's high (1), the float value is negative.
Precision Types:
For PowerPC, there are two types of precisions. Single and Double with Double being more precise. Single Precision floats are 32-bits in width, BUT they are always in a FPR in their 64-bit equivalent form. THIS IS IMPORTANT TO UNDERSTAND. Once again, in the FPRs, all floats are 64-bits in width. For Memory, this is *NOT* the case!
If you see a 32-bit float value in Memory, it's always Single Precision. If you see a 64-bit float value in Memory, it MAY be double precision. More on this shortly.
Here's some examples of 32-bit single floats
Here are those same values, BUT in their 64-bit equivalent form.
Now here is a value that is double precision...
The above value is as close as you can get to 1/3 in double precision. Let's look at what 1/3 is in single precision...
As you can clearly see, single precision is not nearly as precise. Now earlier I said a 64-bit float MAY be double precision. Well how can we quickly tell without using a converter? Simple, look at the 9th thru 16th digits.
If the 10th thru 16th digits are ZERO, *and* the 9th digit is an even hex number, then that 64-bit float is actually single precision.
64-bit Single Float Template:
XXXXXXXXY0000000 #Where Y is an even hex digit
All float values fall under ONE of these categories~
Each category, except QNaN, can be split into sub-categories of positive and negative (i.e. positive infinity and negative infinity). I could go over every category in detail, but with you being a beginner, it's pointless. We really just need to cover the Zero Category.
Positive Zero is well zero...
0x00000000 = 0.0
0x0000000000000000 = 0.0
And negative zero would be...
0x80000000 = -0.0
0x8000000000000000 = -0.0
In all instructions/operations, negative zero has the same effect as positive/regular zero. Therefore if you see negative zero as a result in one of your PowerPC instructions, don't panic. It won't have any ill effects.
One more note:
As mentioned before, the float values in the FPRs are always in 64-bit form. But with GDB, the float values will be displayed to you in all different widths/variations. Just understand that for real hardware, the 64-bit form rule applies.
IMPORTANT: As a precursor, most instructions will have a "single precision" version and a "double precision" version. If a single precision instruction uses double precision inputs, understand that the output will be in single precision (rounding is determined by some bit settings in an SPR known as the Floating Point Status Control Register). Single precision instructions are obviously faster than their double-precision counterparts.
Okay enough babble, onto real instructions!
Floating Point Add:
fadds fD, fA, fB #Single Precision fadd fD, fA, fB #Double Precision
This is what you would expect. fD = fA + fB.
Example fadds instruction--
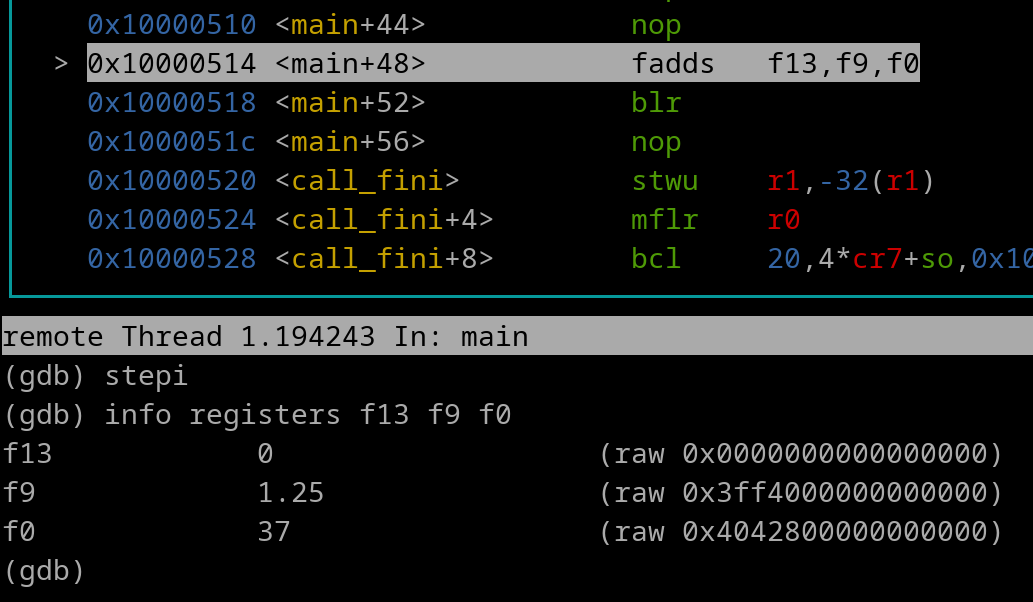
fadds f13, f9, f0 #f13 = f9 + f0
Pretend that...
f0 = 0x0
f9 = 0x0
Here's an image of right before the fadds instruction is going to execute~

Now let's execute the fadds instruction...
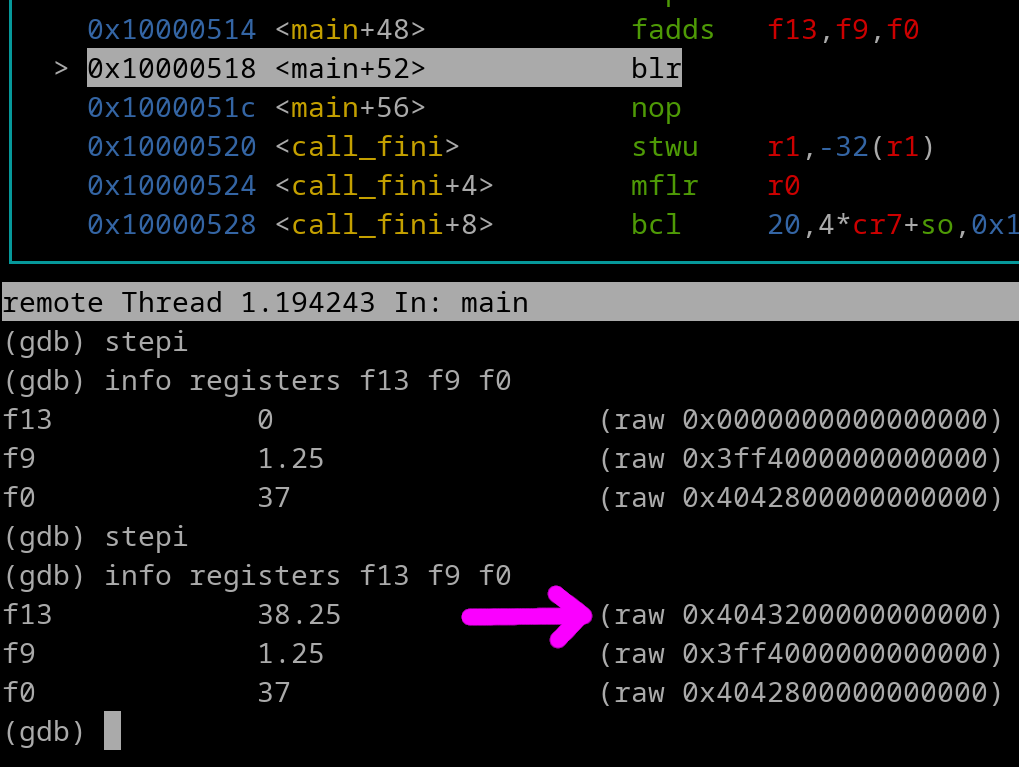
We can see that f13 is 0xXXXXXXXXXXXXXXXX (X.X) because 0.0 + 0.0 = 0.0
Here are some other floating point math instructions.
(s) = if used, then single precision
Floating Point Subtract: fsub(s) fD, fA, fB #fD = fA - fB Floating Point Multiply: fmul(s) fD, fA, fB #fD = fA * fB Floating Point Divide: fdiv(s) fD, fA, fB #fD = fA / fB Floating Point Multiply Add: fmadd(s) fD, fA, fB, fC #fD = (fA * fB) + fC Floating Point Multiply Sub: fmsub(s) fD, fA, fB, fC #fD = (fA * fB) - fC Floating Point Negative Multiply Add: fnmadd(s) fD, fA, fB, fC #fD = -[(fA * fB) + fC] Floating Point Negative Multiply Subtract: fnmsub(s) fD, fA, fB, fC #fD = -[(fA * fB) - fC]
We have some more instructions of math to cover...
Floating Point Reciprocal Estimate:
fres fD, fA #The reciprocal value of fA is placed into fD.
The term "estimate" means the accuracy won't be any more precise than 1/4096. Therefore, the result is always of Single Precision. What is a reciprocal? For example. The reciprocal of 64 is 1/64. Thus if you take the reciprocal of a reciprocal, you get back the original number. What's the purpose of reciprocals? Well division can be slow regarding CPU Speed. So let's say we have the following code.
fdivs f13, f22, f7 #f13 = f22 / f7
It's faster to have the following code instead
fres f7, f7 #f7 = 1/f7 fmuls f13, f22, f7 #f13 = f22 * (1/f7)
Multiplying the reciprocal will yield a similar result in comparison to a typical division. However, you would want to avoid this "trick" if accuracy is important.
Floating Point Square Root:
fsqrt(s) fD, fA #fD = square root of fA
The fsqrt instruction has both single and double precision versions
Floating Point Square Root Reciprocal Estimate
frsqrte fD, fA #The reciprocal of the square root of fA is placed into fD. Accuracy won't be any more precise than 1/4096. Hence the term "estimate". The result is always of single precision.
NOTE: Some PowerPC chips do NOT have a standard fsqrt instruction. For those systems, to get the square root of a number, you need to do the following..
frsqrte fX, fX #Get reciprocal of square root fres fX, fX #Get reciprocal of the reciprocal to get "regular" square root result
This means that for those systems, your square root result will always be of Single Precision.
Let's go over some other common float instructions.
Floating Point Absolute Value:
fabs fD, fA #NOTE: The "s" does *NOT* stand for single precision!
The fabs instruction will simply set bit 0 low of fA and place the result into fD. It's used to change any number to be its positive equivalent. For example..
Floating Point Negative Absolute Value:
fnabs fD, fA #NOTE: The "s" does *NOT* stand for single precision!
The fnabs instruction is basically the opposite of fabs. It will set bit 0 high of fA and place the result into fD. It's used to change any number to be its negative equivalent.
Floating Point Negate:
fneg fD, fA #The negated value of fA is placed into fD.
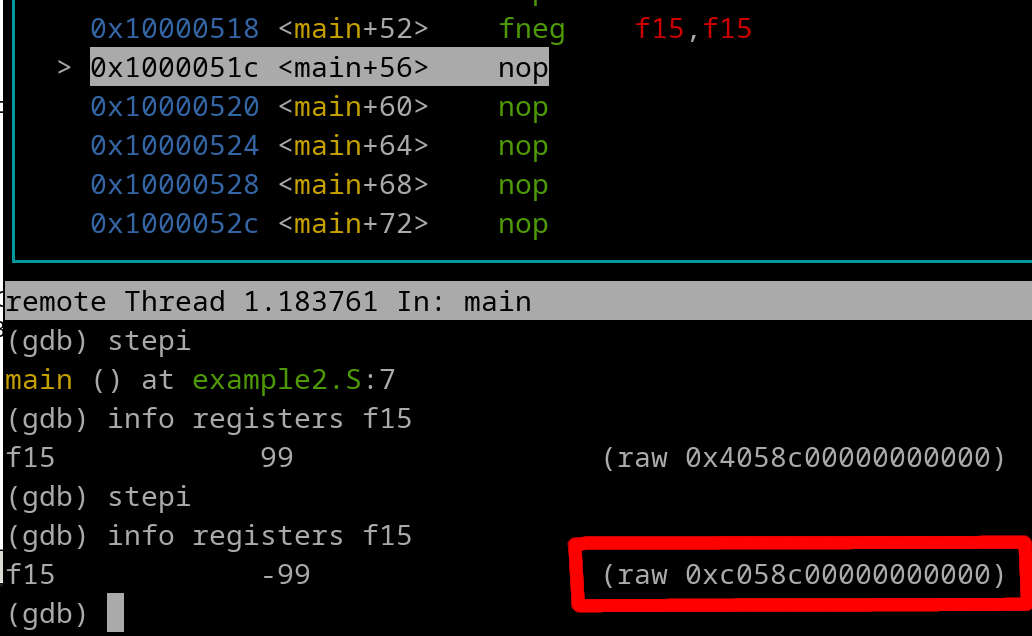
The fneg instruction will simply flip the bit 0 value of fA. fD gets the result. Some examples...
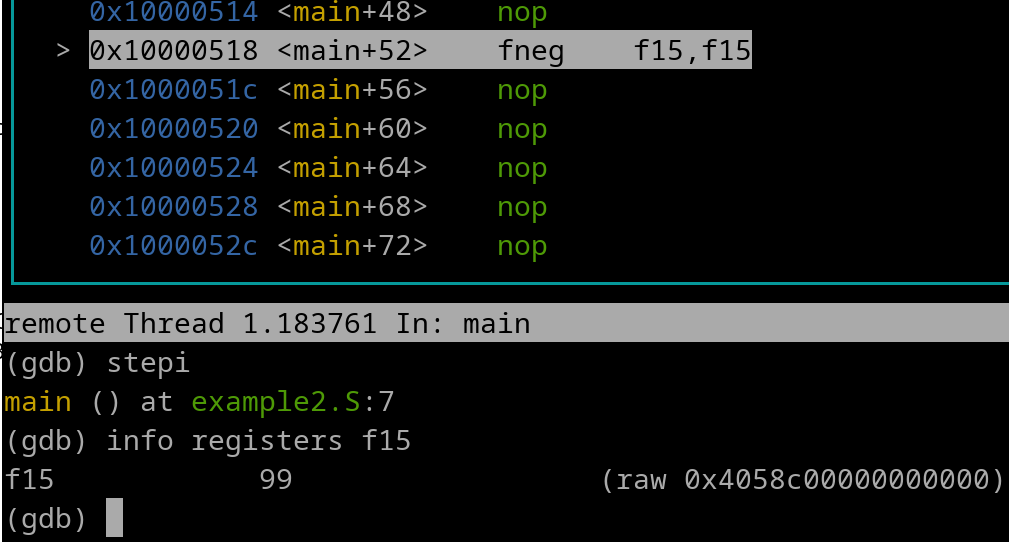
Lets do an example. Pretend that...
f15 =
And we have this instruction...
fneg f15, f15
Here's a pic of right before the instruction was executed..
Now let's execute the instruction...
Here's a couple of more handy instructions...
Floating Point Move Register:
fmr fD, fA #This will copy fA into fD.
Floating Point Round to Single Precision
frsp fD, fA #fA is rounded to single precision and placed into fD.
There are two float comparison instructions at your disposal.
Floating Point Compare Ordered
fcmpo crX, fD, fA
Floating Point Compare Unordered
fcmpu crX, fD, fA
Regardless of what CR field you use, it must explicitly be included in the instruction. If not, the Assembler will reject it.
IMPORTANT: All comparisons are Signed!
Question: Vega, which type of float comparison do I use? Ordered or unordered? How do they differ?
Answer: They differ due to certain bits within the Floating Point Status Control Register (FPSCR) being toggled on/off when a NaN (Not a Number) value is present in the comparison. Since you're a beginner, just stick to Ordered.
IMPORTANT: All float comparisons should use cr1. Technically, it's incorrect to use any other CR field. The reason being is that the FPSCR (in certain scenarios) will output bits of information to cr1 specifically. However for regular/simple float comparisons, cr0 could be used. I recommend always using cr1 because this is what you're suppose to use anyway, and it will instill good habits.
Example fcmpo instruction:
fcmpo cr1, f31, f11 #Compare f31 vs f11 bne- cr1, somewhere #If f31 NOT equal to f11, take the branch to "somewhere"
Common Rookie Mistake....
Because most integer/GPR comparisons use cr0, and because you don't have to explicitly state cr0 in those instructions, it's very easy to forget to explicitly state your CR field for a conditional branch that's after your float comparison.
Example faulty code:
fcmpo cr1, f31, f11 bne- somewhere
The bne instruction is incorrectly checking cr0 when the fcmpo placed its comparison result into cr1. This will cause unpredictable behavior in a program, and will most likely lead to a very hard-to-debug exception.
You may be familiar with the popular Geometry equation of....
a^2 + b^2 = c^2
We will do an exercise where we have the values of "a" and "b", but we need to solve for "c".
Let's pretend our "a" value is 3.125 and resides in f1.
Let's pretend our "b' value is 5.1 and resides in f2.
Let's use f3 for our "c" result
A beginner coder might write it out like this..
fmuls f1, f1, f1 #a^2 fmuls f2, f2, f2 #b^2 fadds f3, f1, f2 #a^2 + b^2 = c^2 fsqrts f3, f3 #f3 = c
The result f3 (c) is ~5.981.
Remember we have the fmadds instruction! We can cut down the Source by 1 line
fmuls f1, f1, f1 fmadds f3, f2, f2, f1 fsqrts f3, f3
Question: Hey Vega, what about f0? Does it have a literal zero rule like r0?
Answer: Nope, not at all.